Vad händer när statistik används mer för att forma opinion än för att beskriva verkligheten? Statistikern Göran Nilsson menar att siffror ofta förvrängs i politiskt maktsyfte.
Politiska beslut baseras dels på mål och värderingar, dels på information om hur verkligheten ser ut och hur den kan påverkas. Informationen om verkligheten bör naturligtvis vara så korrekt och fullständig som möjligt, men i verkligheten kan den vara fabricerad eller förvrängd. Dessvärre använder sig politiker ibland av dessa metoder för att ge en önskad bild av verkligheten för att locka väljare. Då är målet inte att lösa ett samhällsproblem utan snarare att behålla eller komma till makten.
Problemet med fabricerade fakta har uppmärksammats en hel del och jag ska här ge exempel på hur man kan förvränga information av statistisk natur. Här är alltså grundläggande data korrekta, men man använder diverse knep för att ge en falsk bild av verkligheten. Detta kan naturligtvis få lika allvarliga konsekvenser som rena lögner.
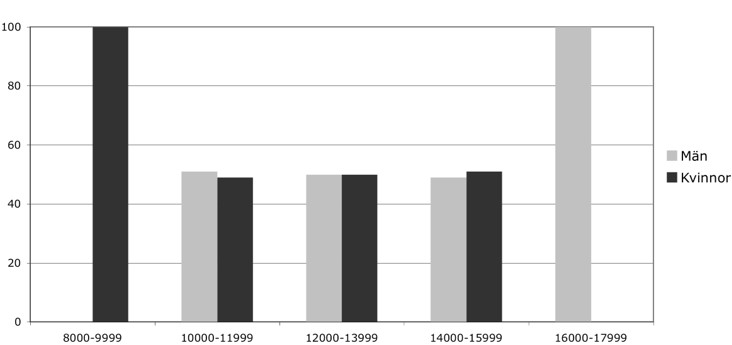
Den kanske vanligaste metoden för att vilseleda med statistik är olämplig grafisk presentation. I figur 1 från min bok Bruk och missbruk av statistik (förlaget 33 sidor) visas ett fiktivt exempel på skillnader i löner mellan kvinnor och män på ett företag. I lägsta löneklassen är det 100 procent kvinnor och i den högsta 100 procent män. Den lägsta löneklassen innehåller bara en person som är en kvinna och den högsta en person som är en man. I själva verket är det samma lönefördelning för kvinnor och män bortsett från att den kvinna som tjänar minst har en krona mindre än den man som tjänar minst och den man som tjänar mest har en krona mer än den kvinna som tjänar mest. Med lämpligt val av gränser för löneklasserna kan man ge intrycket av en sned lönefördelning. Man bör i stället presentera fördelningen på de olika löneklasserna för respektive kön så som visas i figur 2. Här framgår det att det inte är någon större skillnad mellan könen.
Figur 1. Fördelning i procent på kön inom löneklasser.
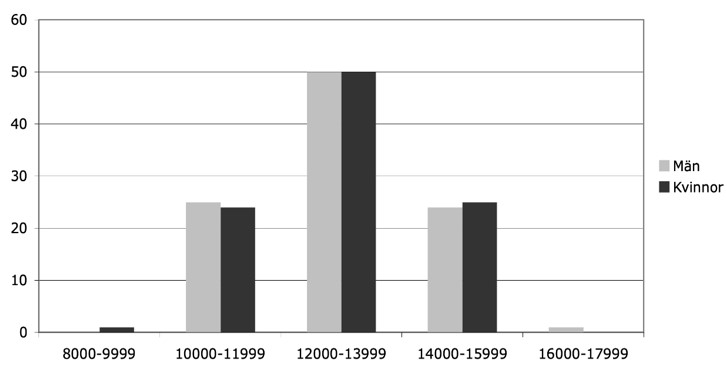
Figur 2. Fördelning i procent på olika löneklasser för män respektive kvinnor.
Rapporteringen om att 33 kvinnor på grund av felaktiga provbedömningar fått sin livmoder bortopererad i onödan på Akademiska sjukhuset i Uppsala har knappast undgått någon. Utöver att en kvinna inte kan bli gravid utan livmoder inträder klimakteriet som kan innebära betydande besvär. En läkare som uttalade sig i tv försökte att tona ner konsekvenserna genom att säga att de inte var så allvarliga eftersom medianåldern (den mittersta åldern) var över 50 år. Medianen säger dock inte något om hur många kvinnor som varit så unga att en bortopererad livmoder varit en katastrof. Nu var åldersspannet för kvinnorna 38–85 år, men flera av kvinnorna kunde lika gärna ha varit under 30 år utan att det påverkat medianen. Ofta används medelvärde eller median för att beskriva en grupp när den relevanta informationen är hur många som är över eller under en viss gräns.
Information är ofta osäker och för att kunna använda den i en beslutssituation måste man ha en uppgift om hur stor osäkerheten kan vara. Vanligen bör man specificera hur stor osäkerhet som kan accepteras. Detta gäller till exempel information som bygger på ett stickprov från en population man vill uttala sig om.
Ett exempel är opinionsmätningar där man tar ett stickprov med syftet att uttala sig om stödet för ett visst parti i hela befolkningen. Skulle vi ta nya stickprov skulle vi förmodligen få olika resultat och spridningen mellan stickproven ger information om osäkerheten i ett enskilt stickprov. Nu behöver vi inte ta flera stickprov för att bedöma osäkerheten. Om stickproven är slumpmässiga kan vi nämligen beräkna vilken spridning vi bör få mellan stickprov från resultatet från ett stickprov. Detta är den grundläggande finessen med att använda statistiska metoder. Från ett stickprov får vi alltså inte bara en skattning av stödet för ett parti utan även en uppgift om osäkerheten i skattningen. Osäkerheten anges vanligen med ett 95-procentigt konfidensintervall, vilket innebär att om man skulle upprepa undersökningen många gånger skulle cirka 95 procent av intervallen innehålla det sanna värdet. Om osäkerheten är för stor kan den minskas genom att man tar ett större stickprov.
Ett annat område där information om osäkerheten är väsentlig är mätningen av olika storheter. Sådana mätningar är sällan felfria och man behöver därför en uppgift om den använda mätutrustningens osäkerhet. För att belysa användningen och tolkningen av osäkerhetsintervall antar vi att jag mäter kroppstemperaturen för att bedöma om det finns en anledning att stanna i sängen. Om termometern visar 38,7 ºC och har en angiven mätosäkerhet på 0,2 ºC så ligger den rätta temperaturen troligen i intervallet 38,5 – 38,9 ºC. Oberoende av var i intervallet den rätta temperaturen ligger kan jag med gott samvete stanna i sängen. Skulle däremot osäkerheten vara 2 ºC skulle de flesta inse att jag inte fått tillräcklig information för ett korrekt beslut. Jag bör investera i en bättre termometer.
Vad gör nu den ansvariga ministern? Jo, hon betraktar helt enkelt det scenario som uppfyller klimatmålet som huvudscenariot och bortser från det andra.
Den korrekta tolkningen av osäkerhetsintervall är att om alla värden inom intervallet leder till samma beslut så har man tillräcklig information. Somliga tycks dock anse att det är tillräckligt att ett önskat värde ligger inom osäkerhetsintervallet eftersom det då inte kan uteslutas. Som exempel kan vi ta regeringens strategi för att uppnå klimatmålet när det gäller utsläpp av koldioxid. Naturvårdsverket har räknat på vad den valda strategin skulle kunna medföra. Eftersom det finns stora osäkerheter så har man kalkylerat ytterlighetsscenarier. Enligt det ena klarar man klimatmålet men enligt det andra ligger man en bra bit ifrån. Jag förmodar att Naturvårdsverket presenterat dessa två scenarier för att ge en uppfattning om osäkerheten. Vad gör nu den ansvariga ministern? Jo, hon betraktar helt enkelt det scenario som uppfyller klimatmålet som huvudscenariot och bortser från det andra.
Eftersom information i samhället ofta är av statistisk natur så har många insett att medborgarna behöver vara statistiskt läskunniga, vilket innebär att de kan tolka och kritiskt utvärdera statistisk information. Detta ämne bör lämpligen läras ut i skolan. Det är inte helt lätt och i en artikel i Statistikfrämjandets tidskrift Qvintensen undrar Karin Landtblom, universitetslektor i matematikämnets didaktik vid Stockholms universitet, hur en statistiker kan hjälpa en icke-statistiker att förstå statistik. Med anledning av denna fråga har Statistikfrämjandet planerat att utveckla olika material som kan bidra till en större förståelse.
Det arbetet kommer dock inte att bli utan problem. Det råder nämligen en konflikt i den akademiska världen om vad man får och inte får göra med statistik. Att använda icke-relevanta statistiska metoder och mått strider mot Statistikfrämjandets etiska kod, där första punkten lyder:
”Analys, tolkning och presentation av statistik ska ske på ett korrekt, transparent och ändamålsenligt sätt. Metoder ska väljas för att ge så tillförlitliga resultat som möjligt och inte utifrån exempelvis förväntningar eller önskade utfall.”
Sådant missbruk av statistik som jag diskuterat i denna artikel ingår dock inte i vad som Nämnden för prövning av oredlighet i forskning (Npof) betraktar som oredlighet. En del akademiska forskare anser till och med att det ingår i den akademiska friheten att använda sådana statistiska metoder och tolkningar som leder till en slutsats som är tillräckligt intressant för en publikation.
Jag tror dessvärre inte att konflikten kommer att lösas förrän man infört ett annat mått på akademisk framgång än antal publikationer.
Göran Nilsson
